A Simple Look at Complex Numbers
Complex what? You’re probably wondering about the title of this article and its significance to cable technology. I’m not referring to “complicated” with the term “complex,” although you might be inclined to think otherwise. Before getting into complex numbers, it will be helpful to look at our number system and its different pieces and parts, starting with the way many of us learned to count during childhood.
Natural numbers—Most of us were taught about natural numbers (sometimes called whole numbers) when we were very young, although I didn’t know they were called that at the time. Examples include 1, 2, 3, 4, 5, and so on. We learned to count with natural numbers: “I have 10 toy cars.” We learned to add them together: “If I have two red gumdrops and three yellow gumdrops, I have five gumdrops.” (2 + 3 = 5). We could sometimes subtract them: “If I have five lollipops and give you two, I still have three lollipops.” (5 – 2 = 3). But occasionally subtraction could get tricky, such as 3 – 5 = ?. Using just natural numbers, there is no answer to this problem, which leads us to integers.
Integers—Integers include natural numbers (1, 2, 3, 4, …), the number 0, and the negation of natural numbers (… –4, –3, –2, –1); the latter many know as negative numbers. Using integers we can calculate an answer to the earlier problem: 3 – 5 = –2, and understand concepts such as temperature. It might be a pleasant +70 °F outside, or a chilly –20 °F.
Rational numbers—Multiplication tables were part of the curriculum in third grade for me, and also some fractions. The latter bring us to the concept of a rational number, which is a number that can be expressed as a quotient or fraction comprising two integers, p/q, where p is the numerator and q is the denominator (and is not zero). Examples include 1/4, 3/8, and 1/10. Even the number –3 is considered a rational number, since it can be expressed as a fraction:
–3/1 for example.
Irrational numbers—These are interesting numbers. One well known example of an irrational number is pi, represented by the symbol π. Pi is a mathematical constant equal to the ratio of a circle’s circumference to its diameter, or about 3.14159. Note that I said “about,” because pi’s decimal representation never ends. It also does not have a permanently repeating pattern.
Real numbers—I found this definition online (Wikipedia): “A real number is a number that can be used to measure a continuous one-dimensional quantity such as a distance, duration or temperature.” Real numbers include natural numbers, integers, rational numbers, and irrational numbers. We can plot real numbers on a number line; an example is shown in Figure 1.

Figure 1. Any real number, including natural numbers, integers, rational numbers (fractions), and irrational numbers (pi is shown), can be plotted on a number line.
All of the aforementioned allow us to solve a variety of mathematical problems and equations. But there are some equations that can’t be solved with just real numbers. An example is a polynomial equation that has no solution in real numbers. That’s where complex numbers can help.
Complex numbers
A complex number is a combination of a real number and an imaginary number. A complex number is expressed in the form a + bi, where a and b are real numbers, and i is the imaginary unit, which is equal to √(-1). Further, a is the real part of the complex number, and b is the imaginary part. If you remember squares and square roots, there is no real number that satisfies √(-1), hence the imaginary unit designation. “Imaginary” here does not mean “pretend.” It’s a legitimate mathematical concept. We need it to handle situations like simplifying √(-4) to 2i.
A quick note about the imaginary unit i: In electronics and engineering, j is often used instead of i, because the letter i (or I) is commonly used to represent electric current. When stating complex impedance, for instance, the form is Z = R + jX, which is discussed later.
Interestingly, a real number a can be considered a complex number a + 0i, whose imaginary part is 0. A purely imaginary number bi is a complex number 0 + bi, whose real part is zero. These two examples can also be stated as a + 0i = a and 0 + bi = bi respectively.
As is the case with real numbers, we can add, subtract, multiply, and divide complex numbers.
Figure 1 shows that it’s straightforward to plot a real number on a number line. But how can we plot a complex number? That’s where what is called the complex plane comes into play; see Figure 2. The figure’s horizontal axis is called the real axis (Re), and the vertical axis is the imaginary axis (Im). I’ve plotted a couple complex numbers, 4 + 3i and –3.5 – 2.5i, as blue dots on the complex plane in Figure 2.
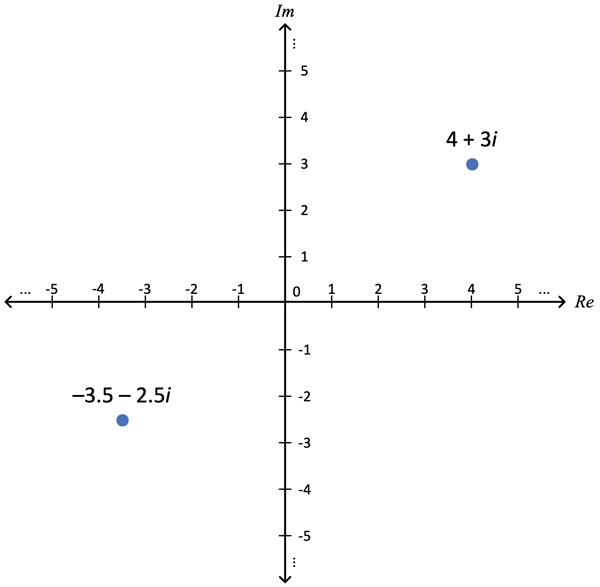
Figure 2. Complex plane showing two complex numbers plotted: 4 + 3i (upper right) and –3.5 – 2.5i (lower left).
Figure 3 shows the complex number a + bi plotted as a red dot in the upper right quadrant of the complex plane. The blue arrow is the complex number’s position vector. Note that the vector has a magnitude (length), which can described by Pythagorean’s Theorem: a2 + b2 = c2. If, for instance, a = 4 and b = 3, then c = 5. The vector also has an angle, which, for this example is arctan(3/4) = 36.87°.
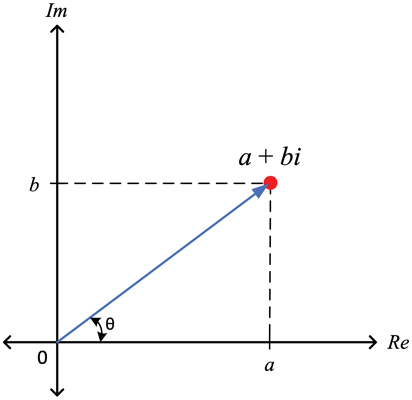
Figure 3. The complex number a + bi is plotted as a red dot.
The blue arrow is the complex number’s position vector.
As you look at Figure 3, does it remind you of anything? How about a quadrature amplitude modulation (QAM) symbol in a data constellation? The Re axis in the figure is equivalent to a data constellation’s in-phase or I axis, and the Im axis is equivalent to the quadrature or Q axis. The red dot is a particular symbol’s position in the constellation. The blue vector’s length is equivalent to the symbol’s magnitude, and the angle θ is its instantaneous phase in degrees. Now we’re talking cable!
Complex impedance
The impedance of a passive device such as a two-way splitter is 75 ohms. Describing it this way suggests something might be missing, though. From SCTE 270 2021r1 Mathematics of Cable: “Impedance in an AC circuit, including RF, is a complex value and includes both resistance (the real part of complex impedance) and reactance (the imaginary part of complex impedance) – that is, both magnitude and phase.”
The missing part of the splitter’s impedance is reactance. It’s highly unlikely that impedance over its operating frequency range is purely resistive.
As mentioned previously, complex impedance is expressed as Z = R + jX, where Z is complex impedance in ohms, R is resistance in ohms, j is the imaginary unit (instead of i), and X is inductive or capacitive reactance in ohms.
Consider a thin lossless half-wavelength dipole antenna in free space; its impedance is Z = 73 + j42.5 ohms. See Figure 4 for a plot of that impedance.
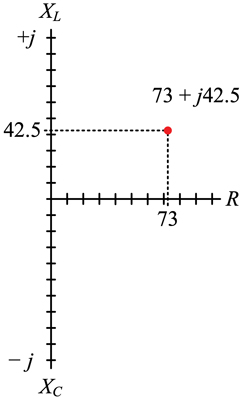
Figure 4. Plot of Cartesian or rectangular form of a thin lossless dipole’s complex impedance in free space (graphic from SCTE 270 2021r1).
Wrapping Up
As you can see, complex numbers really do have significance in cable technology. We may not deal with complex numbers very often, but they certainly play a role in what goes on under the hood. I’ve barely scratched the surface of this topic; if you’d like to learn more, an online search will yield more in-depth information.

Ron Hranac
Technical Editor,
Broadband Library
rhranac@aol.com
Ron Hranac, a 51 year veteran of the cable industry, has worked on the operator and vendor side during his career. A Fellow Member of SCTE and co-founder and Assistant Board Member of the organization’s Rocky Mountain Chapter, Ron was inducted into the Society’s Hall of Fame in 2010, is a co-recipient of the Chairman’s Award, an SCTE Member of the Year, and is a member of the Cable TV Pioneers Class of ’97. He received the Society’s Excellence in Standards award at Cable-Tec Expo 2016. He was recipient of the European Society for Broadband Professionals’ 2016 Tom Hall Award for Outstanding Services to Broadband Engineering, and was named winner of the 2017 David Hall Award for Best Presentation. He has published hundreds of articles and papers, and has been a speaker at numerous international, national, regional, and local conferences and seminars.
Image provided by author.
Shutterstock